Zeno fra Elea er en græsk logiker og filosof, der hovedsageligt er kendt for de paradokser, der er nævnt til hans ære. Der vides ikke meget om hans liv. Hjemby Zeno er Elea. Også i Platons skrifter blev filosofens møde med Socrates nævnt.
Omkring 465 f.Kr. e. Zeno skrev en bog, hvor han skitserede alle sine ideer. Men desværre har det ikke nået vores dage. Ifølge legenden døde filosofen i en kamp med en tyrann (formodentlig lederen af Elea Nearch). Al information om Elea blev samlet bit for bit: fra værkerne fra Platon (født 60 år senere Zeno), Aristoteles og Diogenes Laertius, som tre århundreder senere skrev en bog med biografier om græske filosoffer. Zeno er også nævnt i skrifterne fra de senere repræsentanter for skolen for græsk filosofi: Themisty (4. århundrede A.D.), Alexander Afrodinsky (3. århundrede A.D.) samt Philoponus og Simplicius (begge levede i det 6. århundrede A.D.). Desuden er dataene i disse kilder så godt i overensstemmelse med hinanden, at alle filosofens ideer kan rekonstrueres fra dem. I denne artikel fortæller vi dig om Zeno-paradokser. Så lad os komme i gang.

Paradokser af sættet
Lige siden Pythagoras-æraen blev rum og tid udelukkende betragtet med hensyn til matematik. Det vil sige, de antages at være sammensat af mange punkter og punkter. De har dog en egenskab, der er lettere at fornemme end at definere, nemlig ”kontinuitet”. Nogle Zeno-paradokser beviser, at det ikke kan opdeles i øjeblikke eller punkter. Filosofens ræsonnement koger ned på følgende: ”Antag, at vi har afsluttet divisionen til slutningen. Så er kun en af de to muligheder rigtige: enten får vi de mindst mulige mængder eller dele, der er udelelige, men uendelig i mængde, eller deling vil føre os til dele uden størrelse, da kontinuitet, der er homogen, skal være delbar under alle omstændigheder. Det kan ikke deles i den ene del, men ikke i den anden. Desværre er begge resultater ret latterlige. Den første skyldes, at opdelingsprocessen ikke kan slutte, mens der er dele i resten, der har en værdi. Og den anden skyldes, at i en sådan situation oprindeligt ville helheden være dannet af intet. ” Simplicius tilskrev dette argument til Parmenides, men det er mere sandsynligt, at dets forfatter er Zeno. Vi går videre.
Zenos paradokser af bevægelse
De betragtes i de fleste bøger, der er viet til filosofen, fordi de kommer i dissonans med bevis for eleatikernes følelser. I forhold til bevægelsen skelnes de følgende Zeno-paradokser: "Arrow", "Dichotomy", "Achilles" og "Stages". Og de kom til os takket være Aristoteles. Lad os se nærmere på dem.
"Pil"
Et andet navn er Zeno-kvanteparadokset. Filosofen hævder, at enhver ting enten står stille eller bevæger sig. Men intet er i bevægelse, hvis det besatte rum er lig med det i længden. I et bestemt øjeblik er pilen i bevægelse ét sted. Derfor bevæger det sig ikke. Simplicius formulerede dette paradoks i kort form: ”En flyvende genstand indtager et lige sted i rummet, men det, der indtager en lige plads i rummet, bevæger sig ikke. Derfor er pilen i ro. ” Femistius og Phelopon formulerede lignende muligheder.
"Modsætningsforhold"
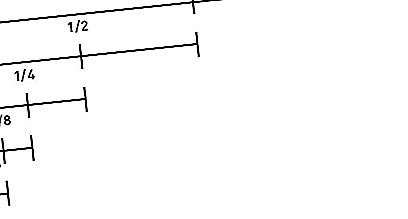
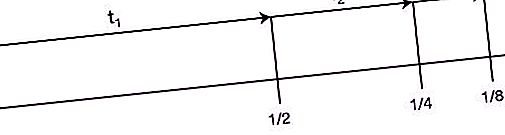
Tager andenpladsen på listen over "Zeno-paradokser". Det lyder som følger: ”Før et objekt, der begynder at bevæge sig, kan rejse en vis afstand, skal det overvinde halvdelen af denne sti, derefter halvdelen af det resterende osv. Til uendelig. Da segmentet under gentagne opdelinger i halvdelen bliver endeligt hele tiden, og antallet af disse segmenter er uendelig, kan denne afstand ikke overvindes i en begrænset tid. Desuden er dette argument både for små afstande og høje hastigheder. Derfor er enhver bevægelse umulig. Det vil sige, løberen vil ikke engang være i stand til at starte."
Dette paradoks kommenterede Simplicius meget detaljeret og indikerede, at der i dette tilfælde skal udføres et uendeligt antal berørelser på et tidspunkt. ”Enhver, der rører ved noget, kan tælle, men det uendelige sæt kan ikke sorteres eller tælles.” Eller, som Philopon udtrykte det, et uendeligt sæt er udefinerbart.
"Achilles"
Også kendt som paradokset for Zeno-skildpadden. Dette er det mest populære filosofiske argument. I dette paradoks af bevægelse konkurrerer Achilles i et løb med en skildpadde, som får et lille handicap i starten. Paradokset er, at den græske kriger ikke vil være i stand til at indhente skildpadden, da han først kommer til stedet for dens start, og hun vil allerede være på det næste punkt. Det vil sige, at skildpadden altid vil være foran Achilles.
Dette paradoks ligner meget en dikotomi, men her går den uendelige opdeling efter progression. I tilfælde af en dikotomi var der en regression. For eksempel kan den samme løber ikke starte, fordi han ikke kan forlade sin placering. Og i situationen med Achilles, selvom løberen begynder at bevæge sig, kommer han stadig ikke løbende noget sted.
"Flock"
Hvis vi sammenligner alle Zeno-paradokser med hensyn til kompleksitet, ville dette være vinderen. Det er vanskeligere end andre at uddybe. Simplicius og Aristoteles beskrev denne begrundelse fragmentarisk, og man kan ikke stole på dens pålidelighed med 100% sikkerhed. Gendannelsen af dette paradoks har følgende form: lad A1, A2, A3 og A4 er bevægelsesløse organer af samme størrelse, og B1, B2, B3 og B4 er organer i samme størrelse som A. B-kroppe bevæger sig til højre, så hver B passerer Og på et øjeblik, som er den mindste tidsperiode af alle mulige. Lad B1, B2, B3 og B4 være organer, der er identiske med A og B, og bevæges i forhold til A til venstre og overvinde hver af kroppene på et øjeblik.
Naturligvis overvinde B1 alle fire organer af B. Lad os tage for en enhed den tid, det tog for et organ af B at gå gennem et organ af B. I dette tilfælde var der brug for fire enheder til al bevægelse. Man troede dog, at de to øjeblikke, der gik for denne bevægelse, var minimale og derfor udelelige. Det følger heraf, at fire udelelige enheder er lig med to udelelige enheder.